

A (when there is no thermal agitation and, therefore, there is no nuclear kinetic energy), the ions adopt distances such that the attractions compensate for the repulsive interactions. Repulsive interactions between ions are essential to the stability of the ionic solid in the absence of repulsive interactions, the cations and anions would unite, ie they would collapse. Repulsive forces due to the overlap of electronic distributions.The dispersion interactions: for ions of limited polarizability this contribution is only about 1% of the electrostatic contribution.The electrostatic attractions and repulsions of the ions.To calculate the reticular enthalpy of an ionic compound it is necessary to consider the different contributions to its energy, such as: Any discrepancy become significant when there is an amount of covalence in the bonds. If the value calculated with the ionic model agrees well with the experimental one, as in this example, it is a reasonable approximation to adopt the ionic model for the compound. The reticular enthalpy allows to evaluate the nature of the bond present in the solid. In this case, the atomization enthalpy of the electron affinity of chlorine must be calculated twice. Īs a last example, in Figure 2, the cycle for the is shown. The reticular enthalpy is the opposite of this enthalpy variation. In this case, the sum of the enthalpies is given by from which. Table 2: The reactions of the Born-Haber for the KCl cycle. Table 2 lists the reactions for the calculation of the energy of formation of the. Therefore, the sum of the enthalpies is given by from which it follows that. Since enthalpy is a function of state, by the law of Hess the sum of the enthalpy variation along a complete cycle must be zero: Figure 1: Born-Haber cycle for caption sodium chloride Table 1: The reactions of the Born-Haber for the NaCl cycle The Born-Haber cycle for the sodium chloride molecular consists of the thermodynamic cycle shown in Figure 1 and with the enthalpy values of the reactions listed in Table I.
The value of is derived from enthalpy data through the Born-Haber thermodynamic cycle.

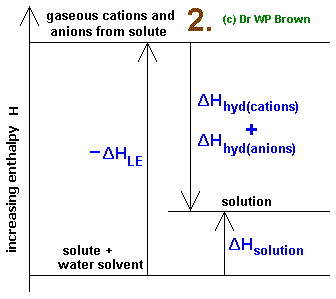
It is highly exothermic and therefore the enthalpy value is negative. The opposite reaction or the formation of the crystal The dissociation of the crystal lattice is endothermic, therefore the values of $ latex $ are always positive. The enthalpy of dissociation of the crystal lattice (or reticular enthalpy,, where stand for crystal) is the standard enthalpy variation that accompanies the formation of an ion gas starting from the corresponding ionic solid: The reticular energetic can therefore be discussed solely on the basis of the lattice enthalpy. The lattice formation process starting from an ion in gas phase is so exothermic that at room temperature (298 K) the entropic contribution can be neglected (the entropic effect due to temperature becomes completely negligible only at temperatures close to absolute zero, ). If is more negative for the formation of the structure than for the structure, the transition will be spontaneous and the solid will have that structure.
#LATTICE ENERGY EQUATION BORN HABER CYCLE FREE#
The stability of a crystal lattice at constant T and P conditions is linked to the Gibbs free energy of lattice formation by the relations My blog in italian on this topics is very popular and for this reason I decided to add an English translation (when I have some free time, I will also translate the text in the Figure and Table).


 0 kommentar(er)
0 kommentar(er)
